Solving Wordle - Novel Strategies for the NP hard problem

Wordle is the popular game where you try to guess a hidden word in $6$ guesses.

Each guess you get a pattern consisting of black, yellow and green colours for each letter of the guess.

A guess of “PARSE” would return a hint with a pattern, like this:

P

A

R

S

E

Terminology

Word	Meaning
Hidden word	A word that could be the answer, but it is hidden from the player
Test word	A word that can be used as a guess
Pattern	The hint given by the game after making a guess
“Easy” mode	The original game where the set of test words is not restricted
“Hard” mode	A variation where the set of test words gets smaller depending on the previous guesses and patterns. In this variation, you can only use guesses that match the patterns provided

Results

The regular wordle list from 15-Feb-22 has $2315$ hidden words $H$, and $12972$ test words $T$.

The regular wordle problem has been looked at in great depth by Alex Selby on The best strategies for Wordle, part 2.

BIGHIDDEN mode, which is a harder version where there are $12972$ hidden words and $12972$ test words, is what I focused on. In particular, the wordle “easy” mode, which is ironically harder to compute than wordle hard mode, where the test words you can use are restricted by your previous guesses.

With BIGHIDDEN mode, it can be proven (by verifying the models) that there are at least $6460$ unique starting test words that have a solution. Unless there are mistakes in the code, there should be exactly $6460$ unique starting test words for this problem, because it was exhaustively calculated.

Finding the solution is quite difficult, but verifying that it is a correct solution is simple. The complete 6460 word list is available here, and the all the models are here.

Using solve from domsleee/wordle.

Goal	Command
Find all solutions	./bin/solve --guesses ext/wordle-combined.txt --answers ext/wordle-combined.txt
Verify a model	./bin/solve --guesses ext/wordle-combined.txt --answers ext/wordle-combined.txt --verify model.json

New strategies

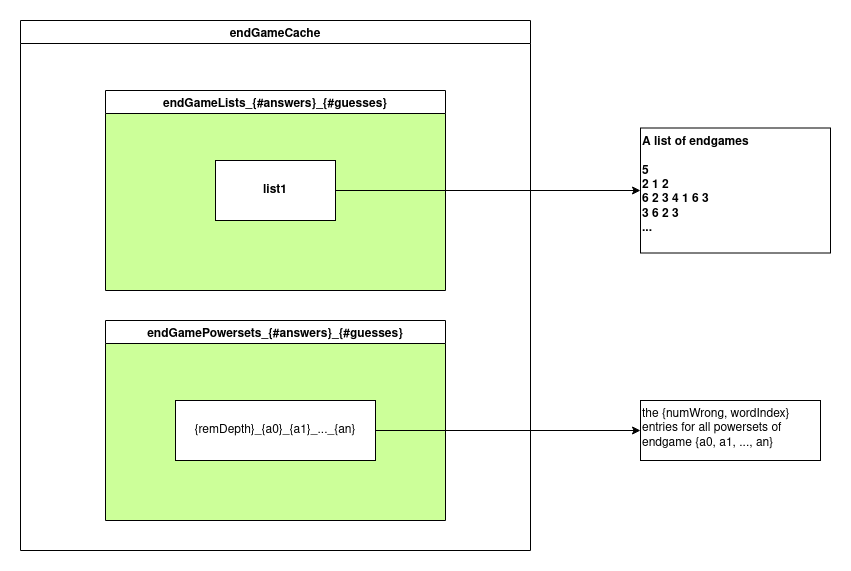
1. EndGame Db

Refer to EndGameAnalysis/ folder.

This is a cutoff that caches all powersets of sets of words $E$. Currently it uses 2276 sets of words that match on 4 letters + positions, e.g. pattern .arks.

2. Lower bounds using a cache entry that is a subset

The main idea is that if you are querying for a lowerbound for a set of hidden words $H$ when you have known lower bounds for sets of hidden words $L = \{H_1,H_2,...,H_n\}$:

$$l = \textrm{max}_{H \in L}\{lb(H) \mid H \subseteq Q\}$$

This only makes sense for easy mode, since for hard mode you would also need to consider the test words.

In terms of implementation details, I tried an inverted index approach SubsetCache.h, and also a trie approach.

3. Most solved in 2 or 3 guesses

See this PR.

We know the following

• 2 guesses ⇒ any 3 words can be solved (by exhaustion)
• 3 guesses ⇒ any 5 words can be solved (reasoning, {1,1,1} can add any 2)

normal: bin/solve --guesses ext/wordle-guesses.txt --answers ext/wordle-answers.txt

bighidden: bin/solve --guesses ext/wordle-combined.txt --answers ext/wordle-combined.txt

--other-program	normal	bighidden
any3in2	✅	✅
any4in2	❌ (13 groups, eg batch,catch,hatch,patch)	❌ (11423 groups)
any6in3	✅	❌ (eg fills,jills,sills,vills,bills,zills)

4. Remove guesses that have a better guess

Refer to RemoveGuessesBetterGuess/

Goal: reduce the size of test words $T$ by removing test words that have a better test word.

Let $\mathcal{P}(H, t)$ be the partitioning of the hidden word set $H$ using test word $t$, i.e.

$$\mathcal{P}(H,t)=\{P(H,t,x)\mid x\in X\}$$

Where $P(H,t,x)$ is the words in $H$ which would give pattern $x$ when guessing the word $t$.

Define $t_1 \geq t_2$ to mean $t_1$ is at least as good as $t_2$ if every partition of $t_1$ is a subset of a partition of $t_2$:

$$\forall_{p_1\in\mathcal{P}(H,t_1)}\exists_{p_2\in \mathcal{P}(H,t_2)}(p_1 \subseteq p_2)$$

$t_1 \geq t_2$ implies that $t_2$ can be deleted from $T$.

proof

Consider this definition of solvability, which returns $1$ iff there is a solution in $d$ guesses:

$$\mathcal{F}(H,d) = \begin{cases} |H|\leq d &d\leq1\\ \text{max}_{t\in T}\prod_{p\in\mathcal{P}(H,t)}\mathcal{F}(p,d-1) &\text{otherwise} \end{cases}$$

We want to prove that $\mathcal{F}(H,d)$ will return an equivalent value if we remove values from $T$.

For every $t_1$ that is used as a better guess than $t_2$:

$$\prod_{p\in\mathcal{P}(H,t_1)}\mathcal{F}(p,d-1) \geq \prod_{p\in\mathcal{P}(H,t_2)}\mathcal{F}(p,d-1)$$

We can prove this by cases:

If any value of the RHS is $0$, the claim is clearly true because the domain is $\{0,1\}$.

If all values of the RHS is $1$, then all values of the LHS is $1$ because every partition of the LHS is a subset of a partition on the RHS.

qed

For least possible guesses

The definition for least possible guesses, taken from The best strategies from Wordle:

$$f(H) = \begin{cases} |H| &|H|\leq1\\ |H|+\text{min}_{t\in T}\sum_{s \ne GGGGG}f(P(H,t,s)) &\text{otherwise} \end{cases}$$

The same definition for “better guess” doesn’t work because the sum can exclude a partition ($s \ne GGGGG$) . So for least guesses, we must add an additional check that $P(H,t_1,GGGGG)=P(H,t_2,GGGGG)$.

Approximation

This is nice however I could not find a fast enough way of doing this.

Using the partitioning approach, I could find an $O(T^2H)$ algorithm, but with a reasonable approximation, there is an $O(T\log{T})$ approach. Typical values are $T = 4000$ and $H = 40$.

An approximation of this partitioning check is to reason about which partitions $p_2$ would be split, by reasoning about how two words of $H$ are differentiated:

1 Non-letter rule

If a letter does not occur in any word of $H$, then any occurrence of that letter in a test word will not differentiate any two words of $H$.

2 Green letter rule

If every position of one letter across all $H$ has the same position in every word of $H$ (for all positions of the letter in the word), then any occurrence of that letter in a test word will not differentiate any two words of $H$.

3 exactly-n letter rule (yellow letter rule)

If there are exactly $n$ occurrences of $c$ in every word in $H$, then any occurrence of $c$ in $T$ that is in a position other than all the positions of $c$ in $H$ can be ignored.

• If there are at most two $c$ in every word in $H$, and one of them is green, the same rule does not apply
  • reason: for guess $t$, 1Y gives no information when $t$ has $1c$ but gives information when $t$ has $2c$. Example: $1Y$ from $2c$ implies $h$ has $1c$

4 most-n letter rule

If there are at most $n$ occurrences of $c$ in every word in $H$, a word $t$ with $≥n+m$ of $c$ can mark up to $m$ positions that don’t occur in any position of $H$ - they are guaranteed to be useless $B$

5 least-n letter rule

If there are at least $n$ occurrences of $c$ in every word in $H$, a word with $t$ with $\le n$ of $c$ can mark all letters that don’t occur in any position of $H$ - they are guaranteed to be useless $Y$